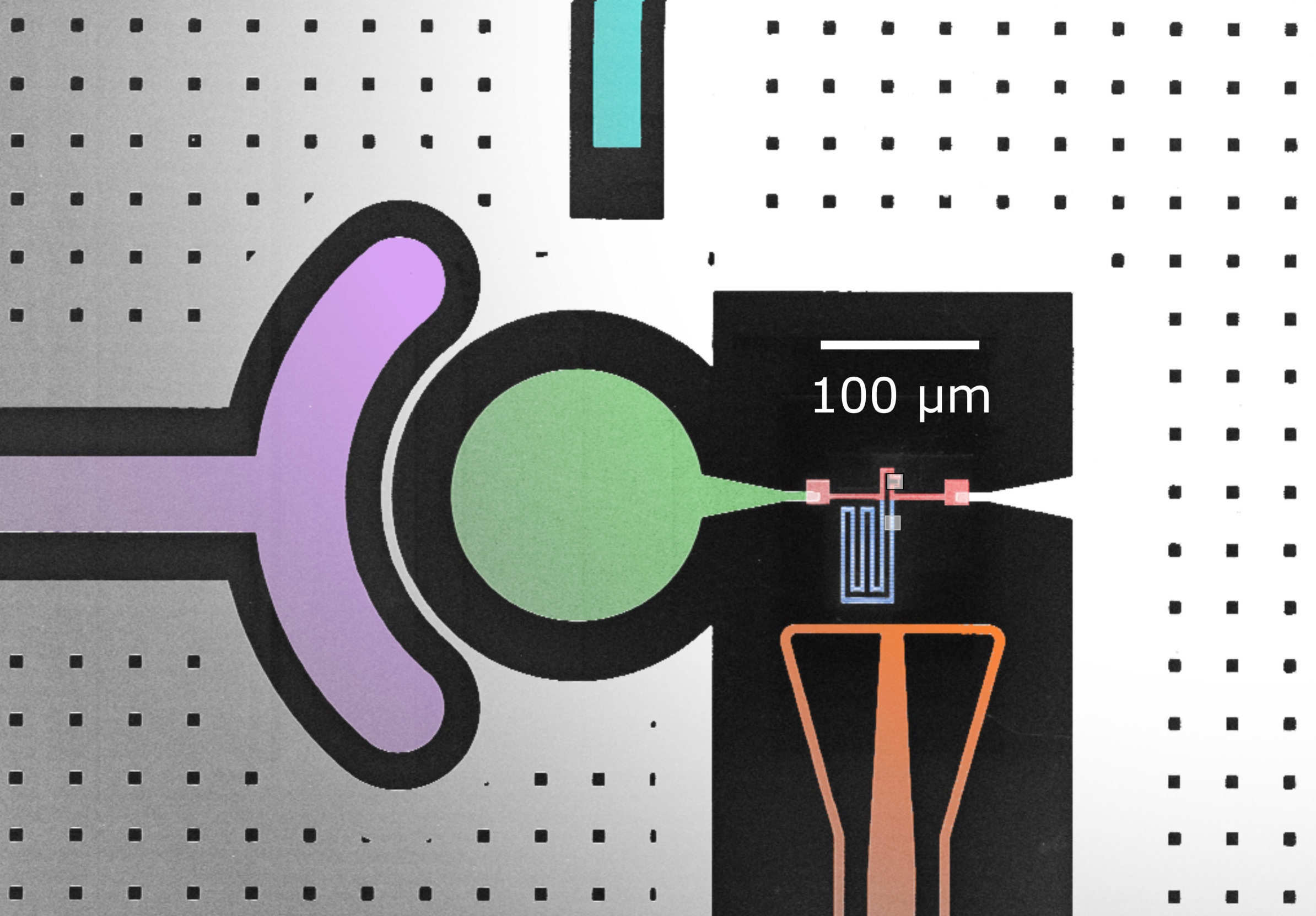
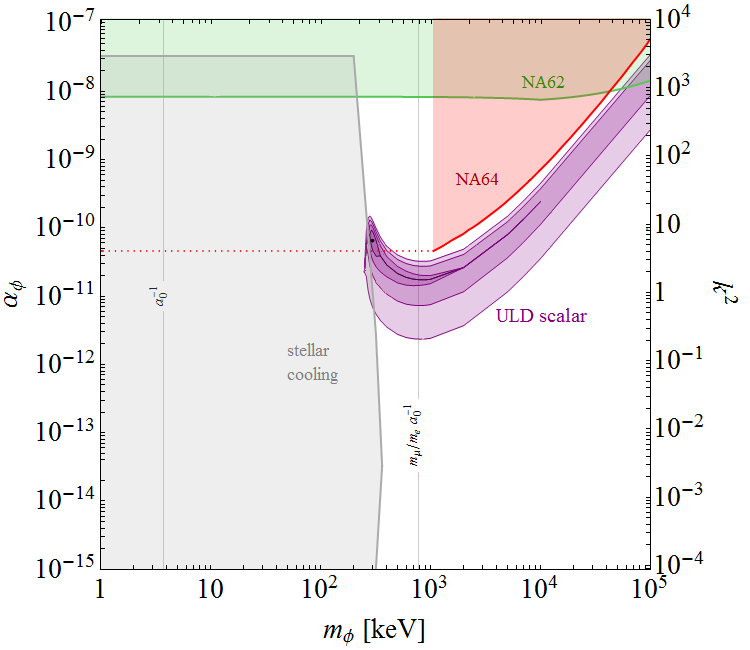
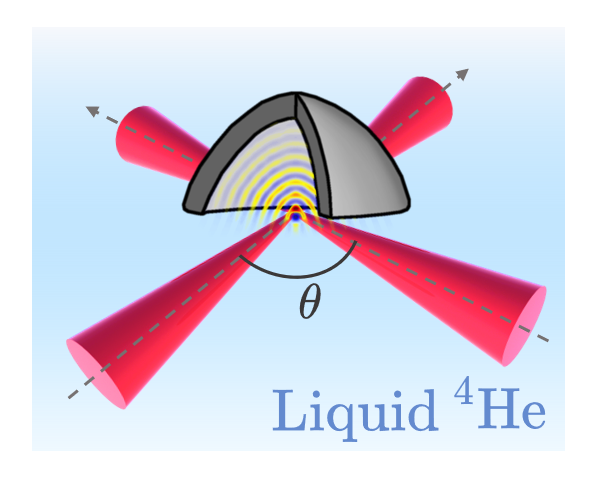
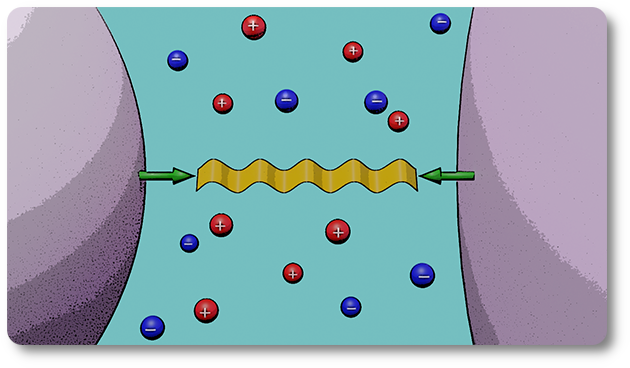
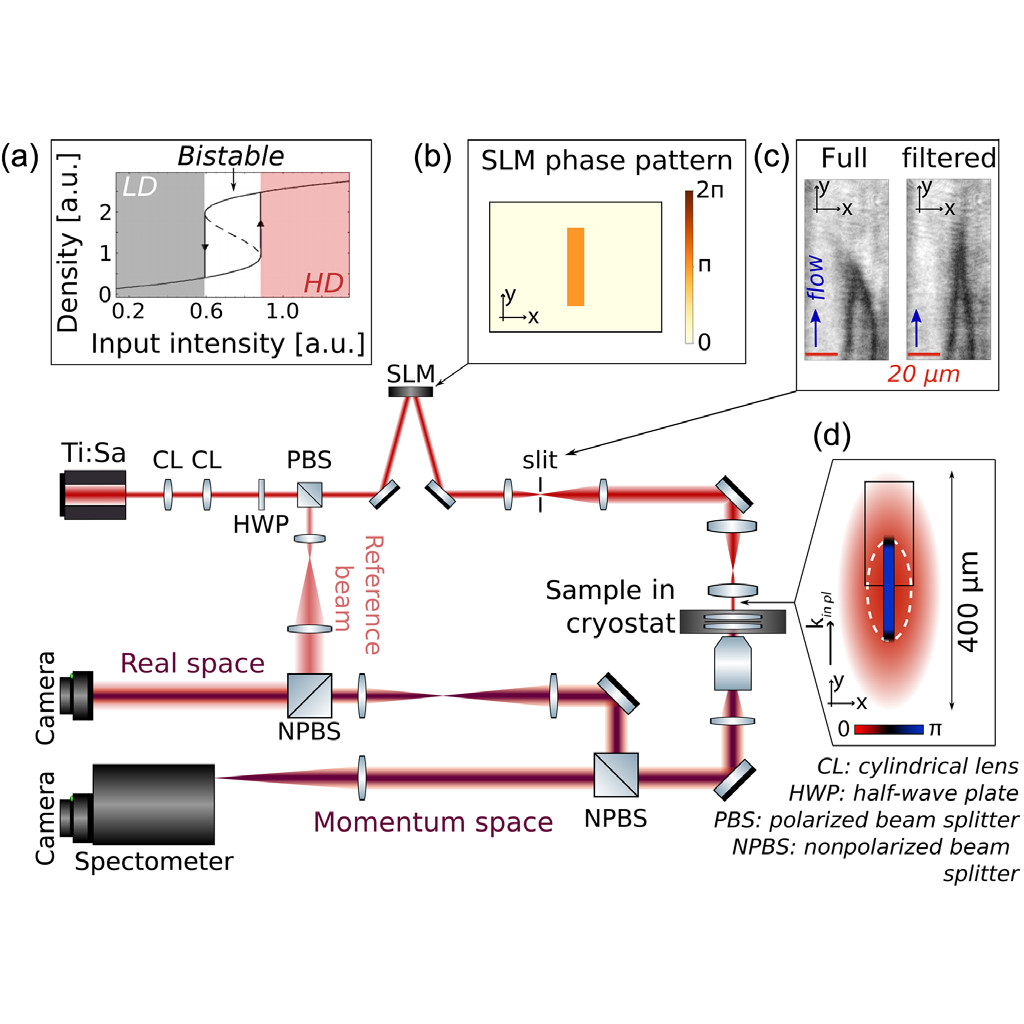
LABORATOIRE KASTLER BROSSEL
Présentation du laboratoireActualités
Axes de Recherche
Le laboratoire Kastler Brossel se compose de 12 équipes regroupées en 4 axes de recherche et un axe transverse.
Agenda
Mercredi 15 novembre 2023. 11h. Mesoscopic physics of photons Hui Cao Department of Applied Physics, Yale University Location : Amphi...
11:00
15/11/2023
Jeudi 16 novembre 2023. Bruno Mansoulié (CEA) La naturalité en physique - vraie ou fausse amie ? Lieu : Sorbonne Université – LKB – Room 210 – ...
14:00
16/11/2023
Mercredi 29 novembre 2023. 11h. Quantum thermalization of large spin atoms in optical lattices Bruno Laburthe-Tolra Laboratoire de Physique...
11:00
29/11/2023
Jeudi 14 décembre 2023. 14h. Franck LALOË (LKB) Trois interprétations différentes de la mécanique quantique, et un petit modèle de synthèse Franck...
14:00
14/12/2023